Я вижу такой алгоритм
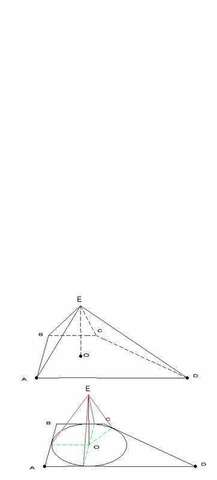
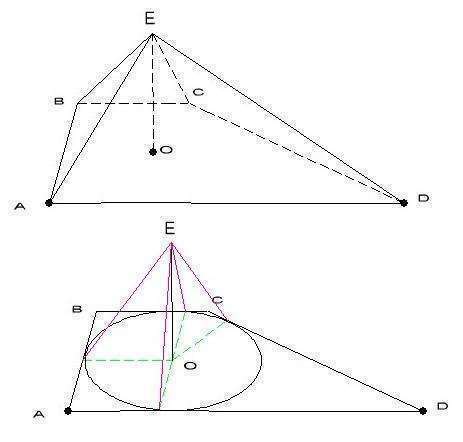
так как все боковые грани наклонены под одним углом, то в трапецию основания можно вписать окружность
центр окружности - проекция вершины пирамиды на основание
надо выразить все стороны трапеции через радиус этой окружности и известный угол у основания
найти радиус по известной стороне основания
найти площадь основания
найти высоту пирамиды
найти периметр трапеции
найти образующую пирамиды
найти площадь боковой поверхности
***********
решение
************
AB=r*2
BC=r*(1+tg(α/2))
CD=r*(tg(α/2)+1/tg(α/2) )
АD=r*(1+1/tg(α/2) ) =2
sin(α) =3/5
cos(α) = 4/5
tg(α/2)=sin(α)/(1+cos(α) ) = (3/5)/(1+4/5 ) = 3/9=1/3
АD=r*(1+1/tg(α/2) ) =r*(1+3 ) =r*4 =2
r=1/2
AB=r*2=1/2*2=1
BC=r*(1+tg(α/2))=1/2*(1+1/3)=2/3
CD=r*(tg(α/2)+1/tg(α/2) )=1/2*(1/3+3 )=5/3
АD=2
S(ABCD)=(BC+AD)/2*AB=(2/3+2)/2*1=4/3
V=1/3*H*S(ABCD)=1/3*H*4/3=H*4/9=(√77)/9
H=(√77)/4
образующая =√(H²+r²)=√(77/16+4/16)=√(81/16)=9/4
S_бок = ½ * образующая * P(ABCD) = ½ * 9/4*(1+2/3+5/3+2)=1/2*9/4*(3+2+5+6)/3=1/2*9/4*16/3=6