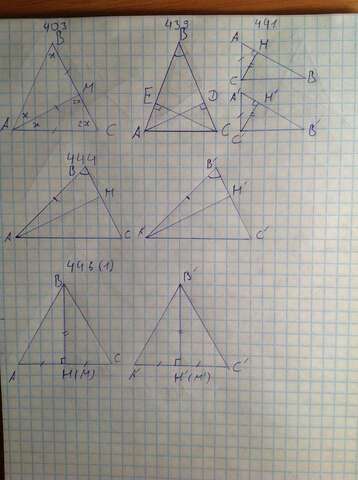
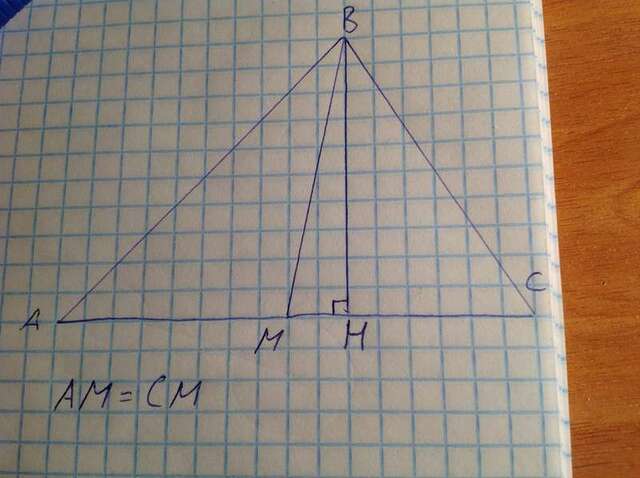403
Пусть угол при основании равен 2x, угол при вершине равен x, так как сумма углов треугольника 180 градусов, 2x+2x+x=180, x=36 - угол при вершине, 2x=72 - угол при основании. Биссектриса AM делит угол A на 2 угла по 36 градусов, тогда треугольники ABM и AMC являются равнобедренными, в первом углы равны 36,36,108, во втором 36, 72, 72. Значит, AM=BM и AM=AC, откуда BM=AC.
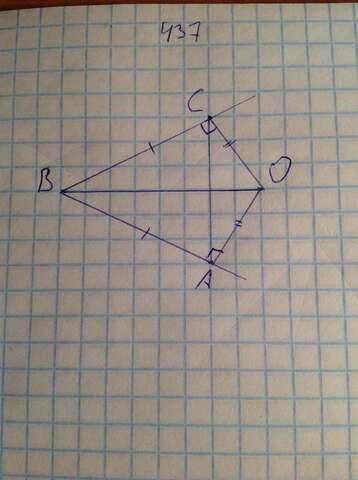
437
По условию, треугольники BCO и ABO прямоугольные. Они равны по катету (AB=BC) и общей гипотенузе OB. Тогда углы между этими сторонами также равны, то есть ABO=CBO. Тогда BO делит угол B на 2 равных угла, то есть BO - биссектриса угла B, что и требовалось.
439
Пусть в треугольнике ABC проведены высоты AD и CE и AD=CE. Прямоугольные треугольники ABD и CBE равны по катету и острому углу. Тогда их гипотенузы AB и BC также равны, что и требовалось.
441
Пусть в прямоугольных треугольниках ABC и A'B'C' углы C, C' прямые, AC=A'C', высоты CH и C'H' равны. Тогда треугольники AHC и A'H'C' равны по катету и гипотенузе, из этого следует, что углы A и A' соответственно равны. Тогда исходные треугольники равны по катету AC=A'C' и прилежащему острому углу A=A', что и требовалось.
444
Пусть в равных треугольниках ABC, A'B'C' проведены высоты AH, A'H'. Прямоугольные треугольники ABH и A'B'H' равны по гипотенузе и острому углу. Значит и соответственные катеты в них равны, то есть AH=A'H'
446
Пусть даны треугольники ABC и A'B'C', в которых BM, B'M' - медианы, BH, B'H' - высоты, AC=A'C', BM=B'M', BH=B'H'.
1 случай - точки M и H совпадают. Тогда треугольники ABH и BCH равны по двум катетам и треугольник ABC равнобедренный. Так как BM=BH=BH'=BM', в треугольнике A'B'C' точки M' и H' также совпадают. Если бы они не совпадали, то в прямоугольном треугольнике B'M'H' гипотенузы B'M' была бы больше катета B'H', а это не так. Значит, оба треугольника равнобедренные с основаниями AC, A'C'. Из того, что AH=A'H'. BH=B'H' следует, что AB=A'B'. Аналогично из того, что CH=C'H' следует, что BC=B'C', тогда треугольники равны по трём сторонам.
2 случай (на рисунке) - точки M и H не совпадают. Из ранее доказанного следует, что M' и H' также не совпадают. Треугольники BMH и B'M'H' равны по катету и гипотенузе, тогда и MH=M'H'. Так как AM=A'M', AH=AM+MH=A'M'+M'H'=A'H'. Тогда треугольники ABH и A'B'H' равны по двум катетам. Аналогично, CH=CM-MH=C'M'-M'H'=C'H', тогда треугольники CBH и C'B'H' равны по двум катетам. Значит, AB=A'B', BC=B'C' и исходные треугольники равны по трём сторонам, что и требовалось.