Способ 1.
Четырехугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых) - параллелограмм.
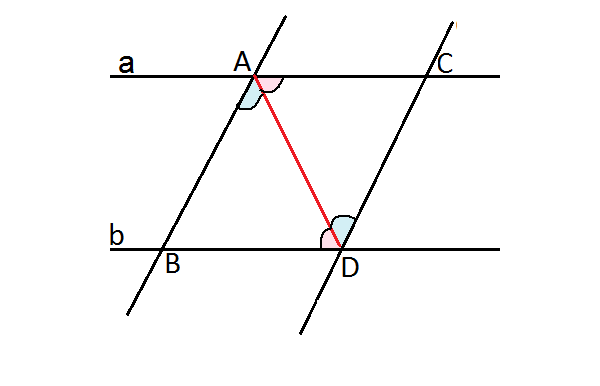
По условию АС и ВD, АВ и CD лежат на параллельных прямых. Следовательно, АВСD- параллелограмм.
В параллелограмме противоположные стороны равны. ⇒
АС=ВD и АВ-СD.
Способ 2.
Соединив А и D, получим треугольники АСD и ABD.
В них накрестлежащие углы при пересечении параллельных прямых а и b секущей АD равны.
Накрестлежащие углы при параллельных прямых АВ и CD секущей АD - равны.
Сторона AD- общая.
Треугольники АСD и ABD равны по второму признаку равенства треугольников. Их соответственные стороны равны.
⇒АВ=СD.