Из точки к плоскости проведены две наклонные, образующие с данной плоскостью углы 30 и 45...

Question

Из точки к плоскости проведены две наклонные, образующие с данной плоскостью углы 30 и 45 градусов. Найдите расстояние между основаниями наклонных, если проекция меньшей наклонной равна 3см, а угол между наклонными прямой.(рисунок+решение) ..заранее спасибо

Comments

кому ты рассказываешь?

---

там без последнего условия ты ни как не найдешь.

---

там как утверждение а угол между наклонными прямой (90)

---

в общем ни знаю как дали задачу так я и написала

---

как у тебя угол между наклонными и прямой может быть 90 градусов?

---

ты думай хоть что пишешь

---

Там не угол между наклонными и прямой ..а просто между двумя наклонными.

---

это меняет дело

---

тогда это просто элементарно.....

---

щас напишу

Answer 1

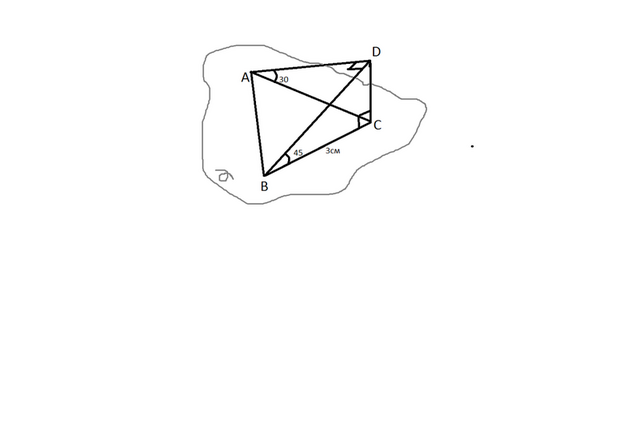
Из условия видно, что у нас образуется пирамида(ABC-основание). Для начала найдем ее высоту:
tg45=1=DC/BC; DC=1*3=3;-высота.
 3 грани в данном случае - прямоугольные треугольники, найдем их гипотенузы:
BD=√(3^2+3^2)=3√2;
AD=DC/sin30=6;
Что мы имеем? 2 катета прямоугольного треугольника ABD, искомая - гипотенуза, найдем ее:
AB=√((3√2)^2+6^2)=3√6 - искомое расстояние.

---

Comments

Сейчас рисунок сделаю

---

Чтобы понятней было

---

Спасибо огромное

---

:)

---

А не поможешь с решением еще одной задачи с рисунком вот решение: прямая мв перпендикулярна стороне ав и высоте вк ромба авсд. Найдите угол между плоскостями мав и мвс, если к-середина стороны ад.