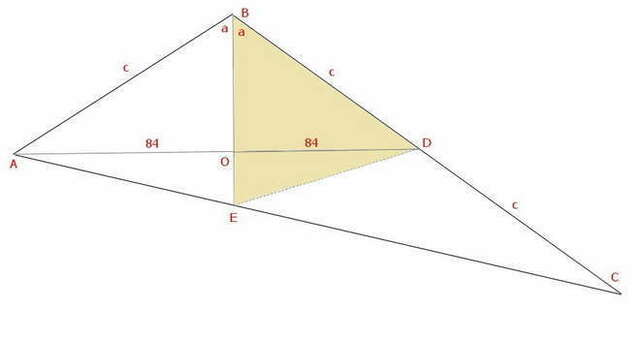
В треугольнике ABD биссектриса ВЕ будет и высотой
---> ABD -- равнобедренный
AB = BD = DC (т.к. AD -- медиана)))
АО = ОD = 168/2 = 84
треугольники АВЕ и DВЕ равны (по двум сторонам и углу между ними)))
их площади тоже равны...
для треугольника ВЕС -- ЕD будет медианой...
медиана делит треугольник на два равновеликих треугольника...
т.е. площади треугольников BED, CED, AEB равны
и = ВЕ*OD/2 = 168*84/2 = 84*84
тогда площадь АВС = 3*84*84
т.к. AD -- медиана, то площади треугольников ABD и ADC тоже равны
и = 3*84*84/2
с другой стороны площадь ABD = 84*ВО ---> ВО = 3*84/2 = 3*42 = 126
по т.Пифагора с^2 = 84*84+126*126 = 2*42*2*42+3*42*3*42 = 13*42^2
c = 42V13 = AB
BC = 2*c = 84V13
OE = 168-126 = 42 ---> АЕ^2 = 84^2 + 42^2 = 5*42^2
AE = 42V5
биссектриса ВЕ делит сторону пропорционально прилежащим сторонам...
АЕ/с = ЕС/(2с) ---> EC = 2*AE
AC = 3*AE = 126V5