1) Фигура вписана в прямоугольник со сторонами 14 на 8 клеточек.
Площадь этого прямоугольника: S = 14*8 = 112 (кл.²)
Не принадлежащие фигуре части прямоугольника:
треугольник S₁ = 2*2/2 = 2 (кл.²)
треугольник S₂ = 4*4/2 = 8 (кл.²)
прямоугольник S₃ = 10*2 = 20 (кл.²)
треугольник S₄ = 4*2/2 = 4 (кл.²)
Общая площадь прямоугольника, не принадлежащая фигуре:
S₁₂₃₄ = 2+8+20+4 = 34 (кл.²)
Площадь фигуры, таким образом:
S₀ = S - S₁₂₃₄ = 112-34 = 78 (кл.²)
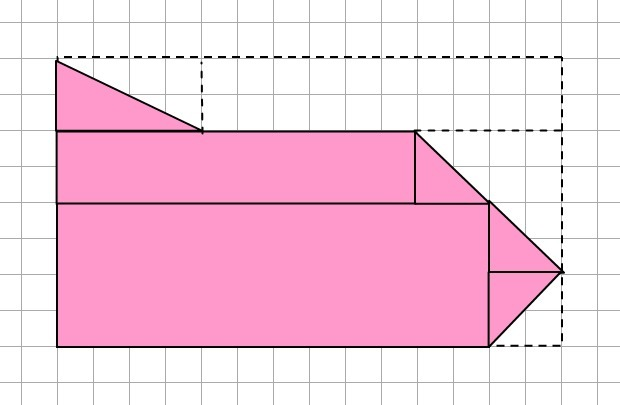
2) Фигура состоит из следующих частей:
прямоугольник S₁ = 4*12 = 48 (кл.²)
3 треугольника S₂ = 3*2*2/2 = 6 (кл.²)
прямоугольник S₃ = 2*10 = 20 (кл.²)
треугольник S₄ = 4*2/2 = 4 (кл.²)
Площадь фигуры: S₀ = S₁+S₂+S₃+S₄ = 48+6+20+4 = 78 (кл.²)
При
вычислении площади данной фигуры удобнее, на мой взгляд, первый способ,
так как считать пришлось меньше. Впрочем, это дело вкуса..))
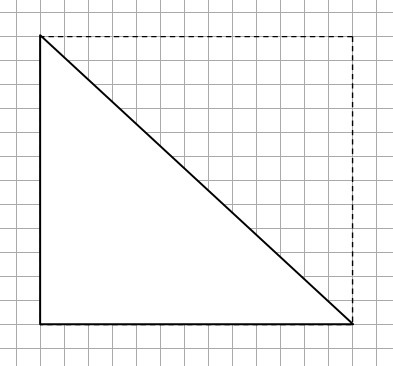
3) См. рис.
Площадь прямоугольника составляет: S = 12*13 = 156 (кл.²)
Площадь полученного прямоугольного треугольника равна половине
площади данного прямоугольника, т.е.:
S₀ = S/2 = 156:2 = 78 (кл.²)
Так как 2 клеточки в длину равны 1 см, то: S₀ = 78:4 = 19,5 (см²)