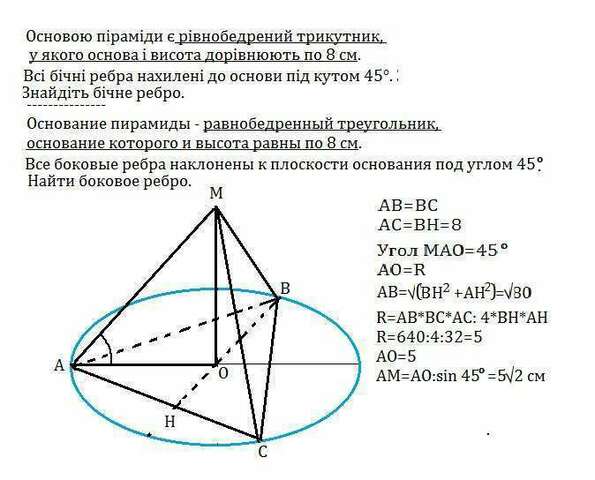
Основою піраміди є рівнобедрений трикутник, у якого основа і висота дорівнюють по 8 см. Всі бічні ребра нахилені до основи під кутом 45°. Знайдіть бічне ребро.
Основание пирамиды - равнобедренный треугольник, основание которого и высота равны по 8 см. Боковые ребра наклонены к плоскости основания под углом 45º. Найти боковое ребро.
Пусть эта пирамида - МАВС.
АВ=ВС, высота ВН основания равна АС=8 см
МО - высота пирамиды.
Ребра пирамиды наклонены под равным углом, следовательно, их проекции равны радиусу описанной вокруг основания окружности. Основание О высоты МО совпадает с центром описанной окружности. Поскольку ребра наклонены под углом 45º, то проекции ребер равны высоте пирамиды МО.
Найдем радиус R описанной окружности.
R=abc/4S, где a,b и c - стороны основания, S - его площадь
Боковые стороны по т.Пифагора:
АВ=√(ВН²+AН²)=√(64+16)=√80
Площадь ∆ АВС=ВН*АС:2=8*8:2=32
R=АВ*АВ*АС: (4*32)=5
В ∆ АОМ ∠ОАМ=45º
АМ=ОА:sin 45=5√2