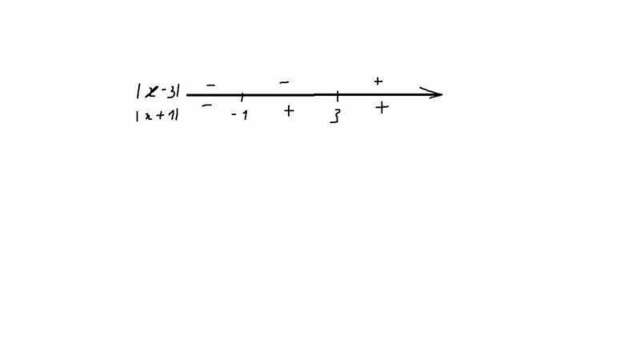889(1)
|x+5| = |10+x|
Равенство имеет место быть тогда и только тогда, когда
x + 5 = 10 + x или x + 5 = -(10+x)
Решаем полученные два уравнения.
Решаем первое:
0 = 5 - нет решений.
Решаем второе:
x + 5 = -10 - x
2x = -15
x = -7.5
И теперь объединяем решения.
Ответ: -7.5
889(2)
|3x+1| = 9 - x
Здесь удобно раскрыть модуль.
Рассмотрим два случая.
1)Если 3x + 1 >= 0, то есть x >= -1/3, то модуль раскрываем со знаком +:
3x + 1 = 9 - x
4x = 8
x = 2
Вышеуказанному неравенству этот корень удовлетворяет, следовательно идёт в ответ.
2)Если 3x + 1 < 0, то есть x < -1/3, то модуль раскрываем со знаком -:
-3x - 1 = 9 - x
-2x = 10
x = -5
x = -5 < -1/3, значит всё нормально.
Ответ: -5;2
890(1)
|x-3| + 2|x+1| = 4
1)Сначала найду нули внутримодульных выражений.
x - 3 = 0 x + 1 = 0
x = 3 x = -1
2)Нанесу на координатную прямую эти нули. Они разбили всю числовую прямую на три промежутка, необходимо определить на каждом из них знак внутримодульного выражения. Рассмотрим самый левый интервал. Возьмём любое число из этого интервала, например, -2. Подставим в оба внутримодульных выражения. Видим, что они оба отрицательны, что отображено на рисунке.
По существу, эти знаки показывают, как мы будем раскрывать каждый модуль на соответствующем интервале.
Аналогично определяем знаки обоих выражений на остальных интервалах.
3)Рассмотрим уравнение на полученных трёх интервалах.
1)Если x <-1, тооба модуля раскрываем со знаком -. Получаем уравнение:<br> 3 - x -2(x+1) = 4
3 - x - 2x - 2 = 4
-3x = 3
x = -1
x = -1 не удовлетворяет условию x<-1, поэтому на первом интервале уравнение решений не имеет.<br>2)Если -1<=x<=3, то мы видим по рисунку, что первый модуль раскрывается со знаком -, а второй со знаком +. Получаем уравнение:<br> 3 - x + 2(x+1) = 4
3 - x + 2x + 2 = 4
x = -1
x = -1 входим в рассматриваемый интервал. Поэтому на втором интервале уравнение имеет корень x = -1.
3)Наконец, если x> 3, то видно, что оба модуля раскрываются со знаком +. Получаем уравнение:
x - 3 + 2(x+1) = 4
x - 3 + 2x + 2 = 4
3x = 5
x = 5/3
Легко видеть, что x = 5/3 не удовлетворяет условию x > 3, значит, на этом интервале корней также нет.
Ну и теперь просто собираем все решения со всех интервалов, если они есть.
Получаем ответ: -1
Аналогичным образом решается последнее уравнение.