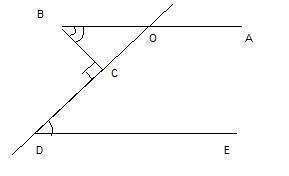
С1.1. Продолжим сторону DC до пересечения с прямой АВ. По условию АВ и DE параллельны, значит углы ВОС и EDC равны как накрест лежащие углы при пересечении двух параллельны АВ и DE секущей DC.
2. Пусть угол EDC равен х, тогда угол АВС будет 2х. 3. Треугольник ВСО - прямоугольный по условию. Зная, что сумма углов треугольника равна 180°, составим уравнение для него:
2x + х + 90 = 180
3х = 90
х=30
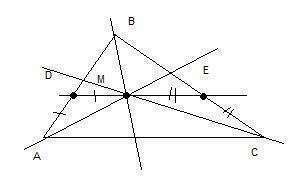
C2.1. Поскольку DE II AC, то 2. Поскольку треугольник ADM равнобедренный по условию, то его углы DAM и DMA при основании равны, но 3. Углы ЕМС и МСА равны также как накрест лежащие углы при пересечении двух параллельных прямых DE и АС секущей СМ: <ЕМС = <МСА.<br>4. Треугольник МЕС равнобедренный по условию также, и его углы при основании ЕМС и ЕСМ равны:
5. Прямая МВ пересекается с биссектрисами МА и МС в одной точке, значит МВ также биссектриса (в любом треугольнике биссектрисы пересекаются в одной точке).Таким образом, прямые МА, МВ и МС делят углы треугольника как биссектрисы пополам в отношении 1:1.