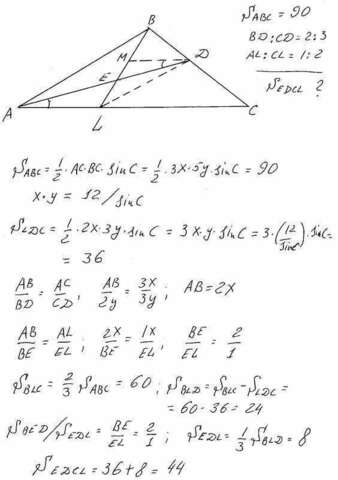
Обозначим единицу пропорции Х, У. Тогда АL=1Х, СL=2Х, ВД=2У, СД=3У. (смотри рисунок).Далее находим площадь LДС=36, и ВLC=60-поскольку высоты треугольников АВL и ВLС равны то их площади относятся как их основания. Затем воспользуемся свойством биссектрисы и найдём отношение ВЕ/ЕL=2/1. Также относятся и площади треугольников ВЕД и ЕДL. Ответ Sедсl=44. Но это не сложное решение, во втором варианте приводится решение, когда мы не знаем , что АД-биссектриса. Тогда проводим МД параллельно АС и далее из подобия треугольников МЕД и АЕL находим необходимые соотношения. Треугольники эти подобны по трём углам. Ответ тот же Sedcl=44.