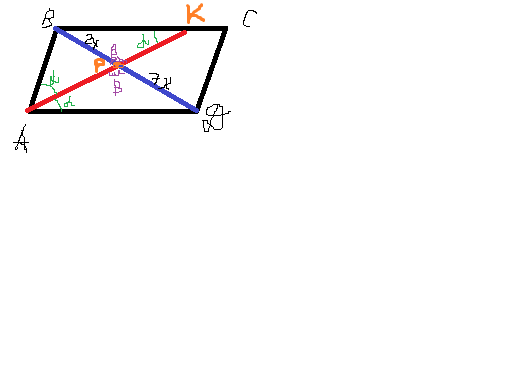
1.Разберемся с углами: угол ВАК=КАD(т.к. АК-биссектриса), обозначим эти углы за α, просто для упрощения жизни.
угол BKP=KBP=α, т.к. прямые АВ и СD параллельны, то эти углы накрест лежащие.
2. Найдем подобные треугольники
ΔВРК подобен ΔАРD по трем углам, значит, можем записать равенство:
BP:PD=BK:AD=2:7 ⇒
BK=(2/7)*AD
3. АD=BC(т.к. параллелограмм)
BC=BK+KC
AD=BK+KC
KC=AD-BK=AD- (2/7)AD=(5/7)AD
4. Т.к. АD=ВС, то КС= (5:7)ВС
Значит, точка К делит сторону ВС 5:7