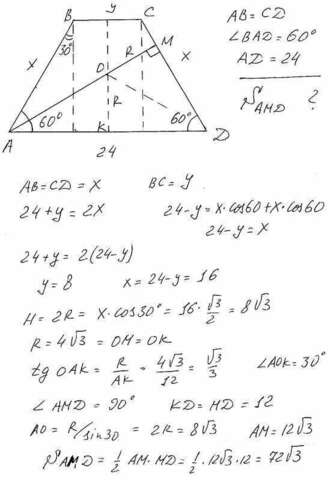
Обозначим трапецию АВСД. Стороны Х и У. Поскольку в трапецию можно вписать окружность-сумма боковых сторон =сумме оснований. Отсюда два уравнения из которых находим Х и У.Далее высоту Н=2R. Поскольку угол АОК=30 градусов а угол АДМ=60 градусов, то треугольник АМД-прямоугольный. О-центр вписанной окружности, но раз ОМ перпендикулярно СД, значит ОМ-радиус. Тогда из равенства треугольников ОКД и ОМД (по катету и гипотенузе) находим МД=12. Затем АМ и окончательный ответ S амд=72 корня из 3.