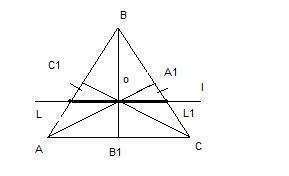
Зная, что медианы треугольников пересекаются в одной точке, которая делит их в отношении 2:1, считая от вершины, запишем:
ВО/ОВ1=2/1, отсюда
ОВ1=ВО/2=24/12 = 12 см.
ВВ1=24+12=36 см
Треугольники С1ВО и АВВ1 подобны по первому признаку подобия: два угла одного треугольника соответственно равны двум углам другого. В нашем случае ВО/ВВ1=LO/AB1
АВ1=АС/2=9√2/2=4.5√2 см, т.к. в ВВ1 - медиана
24/36=LO/4.5√2, отсюда
LO=24*4.5√2/36=3√2 см
Поскольку медиана ВВ1 делит LL1 пополам, то
LL1=LO*2=3√2*2=6√2 см