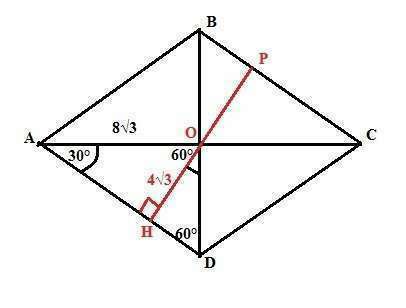
Диаметр вписанной в ромб окружности равен его высоте.
РН=8√3, ОН=ОР=4√3,а его диагональ равна 16√3 (дано).
Диагонали ромба взаимно перпендикулярны, являются биссектрисами углов и точкой пересечения делятся пополам. Следовательно, отрезок ОD или AO равен 8√3.
Предположим, что диагональ BD=16√3. Тогда Но Значит диагональ АС=16√3.Тогда в прямоугольном треугольнике АОН имеем: гипотенуза АО=8√3, катет ОН=4√3.
Найдем катет АН=√(64*3-16*3)=12.
В прямоугольном треугольнике DОН имеем:
HOD=30° и OD=2*HD. Тогда по Пифагору: 4HD²-HD²=ОН² или 3HD²=48 HD²=16.
Отсюда HD=4.
Или так: высота ОН из прямого угла 48=12*HD и HD=4.
Тогда сторона ромба AD=AH+HD=12+4=16.
Периметр ромба 4*16=64.
Ответ: Р=64.