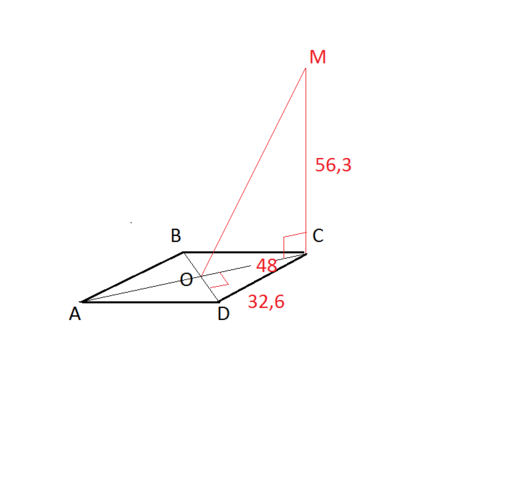
Сделаем построение по условию
искомое расстояние ОМ
сторона ромба DC = 32,6 см
диагонали ромба пересекаются под углом 90 град
ODC - прямоугольный
< ОСD = 1/2 <BCD = 1/2 48 = 24 град<br>ОС = DC*cos24 = 32,6*cos24
MC перпендикуляр к плоскости ромба
АС лежит плоскости ромба, значит МС перпендикулярна ОС
ОС - проекция наклонной МО на плоскость ромба
три точки ОСМ образуют плоскость ОСМ
треугольник ОСМ прямоугольный
по формуле Пифагора
OM^2 = OC^2 +MC^2
OM = √ ОС^2 +MC^2 = √ ( (32,6*cos24)^2 + 56.3^2 ) = 63,7 см
ответ 63,7 см