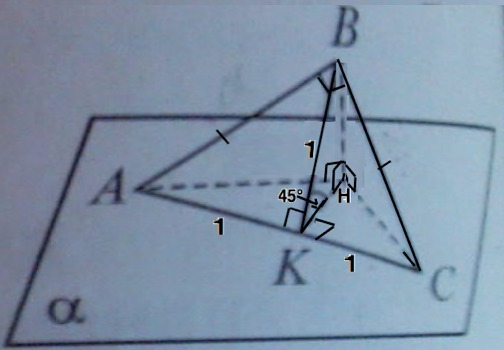
∆ АВС прямоугольный равнобедренный.⇒ его острые ∠А и ∠С равны 45°.
Углом между двумя плоскостями является угол, сторонами которого являются лучи с общим началом на линии их пересечения, которые проведены в его гранях перпендикулярно этой линии.
На рисунке это угол ВКН, т.е. угол между наклонной ВК и её проекцией и по условию он равен 45°, которые по т. о 3-х перпендикулярах обе перпендикулярны гипотенузе АС.
Примем АС=2. Тогда медиана ВК равнобедренного ∆ АВС=АС:2=1
КН - проекция ВК на плоскость α и, т.к. угол ВКН=45°, ВН=КН=ВК•sin45°=0,5√2
АВ=ВК:sin45°=√2
sin угла ВАН=ВН:АВ=0,5√2:√2=0,5 - это синус 30°.
Ответ– вариант 2) 30°