Найдите стороны и углы параллелограмма, если его периметр равен 40 см, а высота...

Question

Найдите стороны и углы параллелограмма, если его периметр равен 40 см, а высота параллелограмма и биссектриса его угла, проведенные из одной вершины, делят сторону параллелограмма на три равных отрезка.
P.S. Напишите решение, а не просто ответ :)

Answer 1

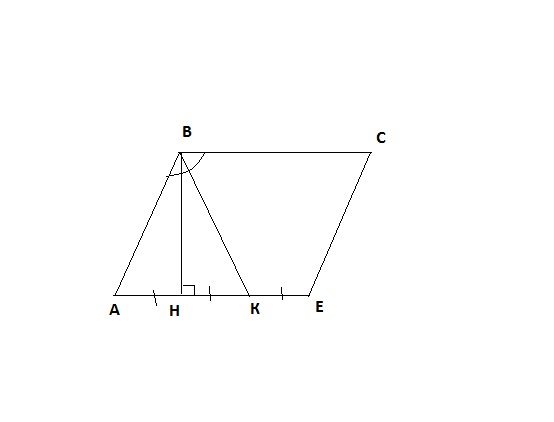
Углы АКВ и СВК равны как накрест лежащие при пересечении двух параллельных прямых АЕ и ВС секущей ВК. Но по условию В треугольнике АВК высота ВК является также и медианой, треугольник АВК - равнобедренный, и Пусть равные отрезки АН, НК и КЕ будут х. Тогда в треугольнике АВК:
АК=АВ=2х
Таким образом, стороны параллелограмма равны:
АВ=2х, АЕ=3х
Зная периметр параллелограмма, запишем:
(2х+3х)*2=40
4х+6х=40
10х=40
х=4
АВ=2*4=8 см АЕ=3*4=12 см
В равностороннем треугольнике °