S = h*AB = DO*AB
1. Найдем ВС:
ВС = ВЕ+ЕС = 7+3 = 10 см
2. Найдем угол DAB:
DAB = (360 - 150*2) : 2 = 30°
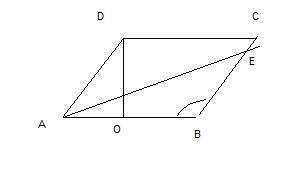
3. Построив высоту DO, получаем прямоугольный треугольник AOD. Зная, что катет прямоугольного треугольника (в нашем случае это DO), лежащий против угла 30 градусов равен половине гипотенузы (это AD), находим DO:
DO = AD : 2 = BC : 2 = 10 : 2 = 5 см
4. Рассмотрим треугольник АВЕ. Угол В по условию 150. Т.к. АЕ - биссектриса, то угол ЕАВ равен половине угла DAB:
EAB = 30 : 2 = 15°
Находим оставшийся неизвестный угол АЕВ треугольника АВЕ:
АЕВ = 180 - 15 - 150 = 15°
Таким образом, треугольник АВЕ - равнобедренный, т.к. углы при его основании АЕ равны. Значит, АВ = ВЕ. АВ = 7 см.
5. Находим площадь параллелограмма:
S = DO*AB = 5 * 7 = 35 см²