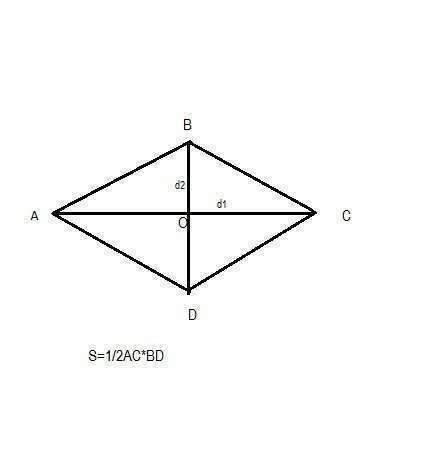
Площадь ромба равна половине произведений диагоналей:
S=d₁*d₂/2, где
d₁,d₂ -диагонали ромба
Диагонали ромба АС и ВD делят его на 4 равных прямоугольных треугольника.
Рассмотрим Δ АВО
Гипотенуза в нем равна АВ=5см, а катет равен половине диагонали АО=АС:2=8:2=4 см
По теореме Пифагора найдем второй катет ВО, который является половиной второй диагонали, т. к. диагонали в точке пересечения делятся пополам.
АВ²=ВО²+АО²
5²=ВО²+4²
25=ВО²+16
ВО²=25-16=9
ВО=√9=3 см
Значит ВD=2*ВО=2*3=6 (см)
Площадь ромба равна половине произведения диагоналей:
S=1/2d1d2=1/2*АС*BD=6*8=24 (см²)
Ответ: площадь ромба равна 24 см²