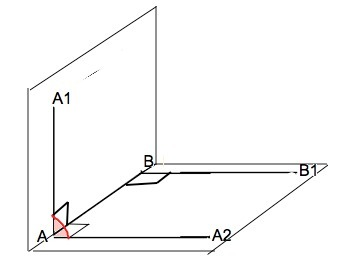
Прямые АА1 и ВВ1 лежат в разных плоскостях и не пересекаются. Эти прямые - скрещивающиеся.
Проведем АА2 параллельно ВВ1. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой. ⇒
ВВ1 перпендикулярна АВ, следовательно, АА2 перпендикулярна АВ . Угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, проведенные в его гранях перпендикулярно ребру, является линейным углом двугранного угла. Отсюда следует, что, если АА1 перпендикулярна ВВ1, она перпендикулярна АА2, и тогда
искомый двугранный угол - угол А1АА2, и он равен 90°.