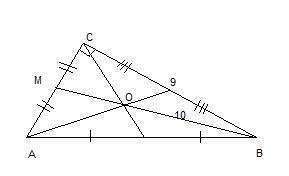
Зная, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины, запишем:
ОВ : ОМ = 2 : 1, отсюда
ОМ = ОВ*1 : 2 = 10:2= 5 см,
ВМ = 10+5=15 см
В прямоугольном треугольнике МСВ по теореме Пифагора найдем катет СМ:
CM=√BM²-BC²=√225-81=√144=12
Т.к. ВМ - медиана, то АС=СМ*2=12*2=24
Площадь прямоугольного треугольника равна половине произведения его катетов.
S=AC*BC:2=24*9:2=108