1) sinx>1/3
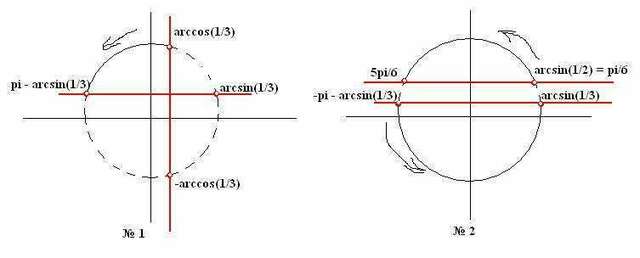
cosx<1/3<br>Решим с помощью единичной окружности (см. рисунок):
Найдем на рисунке пересечение, отметим точки пересечения прямых y=1/3 и x=1/3 с окружностью.
Получаем ответ: arccos(1/3) + 2πk < x < π - arcsin(1/3) + 2πk, k∈Z<br>Вариант ответа А.
2) 7sin^2(x) + cos^2(x) > 5sinx
7sin^2(x) + 1 - sin^2(x) - 5sinx > 0
6sin^2(x) - 5sin(x) + 1 > 0
Замена: sinx = t, t∈[-1;1]
6t^2 - 5t + 1 > 0
t1 = 1/3, t2 = 1/2
t<1/3 и t>1/2
sinx<1/3, sinx>1/2 - решим два неравенства (не система!), пересечения на окружности искать не нужно (см. рисунок). Отмечаем точки пересечения прямых y=1/3 и y=1/2.
Получаем: π/6 + 2πk < x < 5π/6 + 2πk, -π - arcsin(1/3) + 2πk < x < arcsin(1/3) + 2πk<br>Вариант ответа D