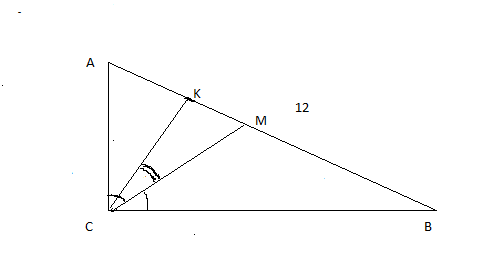
1) Дан треугольник АВС, угол С - прямой. СM- биссектриса, СК- высота(см рисунок)

значит

Из прямоугольного треугольника АСК

Значит АС=6 см, СВ=6·√3
2) Дан треугольник АВС, угол С - прямой. СM- биссектриса ( см тот же рисунок)
По условию АМ:МВ=3:4
Свойство биссектрисы угла треугольника: биссектриса угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам.
АС:ВС=АМ:МВ=3:4
Пусть АС=3х, тогда ВС=4х.
По теореме Пифагора АВ=5х=√(3х)²+(4х)²
Периметр Р=3х+4х+5х=12х, а по условию задачи 84 см.
12х=84,
х=7
Тогда стороны треугольника АС=21 см, ВС=28 см, АВ=35 см.