Диаметры AB и CD данного круга взаимно перпендикулярны. ** дуге ACB взяты произвольные...

Question

Диаметры AB и CD данного круга взаимно перпендикулярны. НА дуге ACB взяты произвольные точки P и Q, а внутри круга проведена дуга AB окружности с центром в точке D. Хорды DP и DQ пересекаются с этой дугой соответственно в точках M и N, точки P1 и Q1 - основания перпендикуляров, проведённых из точек P и Q к прямой AB. Докажите, что площадь криволинейного четырёхугольника PQNM равна площади треугольника DP1Q1

Comments

Вообще-то это устная задачка.

Answer 1

БЕЗ ОГРАНИЧЕНИЯ ОБЩНОСТИ достаточно доказать это, если точка Q совпадает с точкой C. 
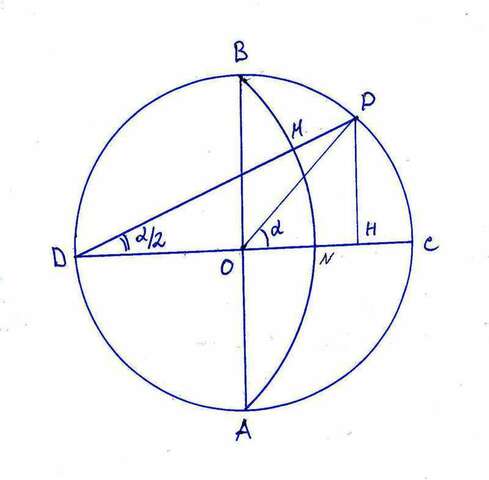
На чертеже видно, что площадь NMPC равна 
Snmpc = Sdpc - Sdpn;
Имеются ввиду фигуры с указанными вершинами, ограниченные линиями, присутствующими на чертеже. К примеру, Sdpn - это площадь сектора окружности с центром в точке D. Радиус этой окружности DB = R√2; где R = OC; - радиус окружности с центром в точке О.
Фигура DPC радиусом OP делится на равнобедренный треугольник DOP и сектор меньшей окружности POC. 
Если принять ∠POC = α, то ∠MDN = α/2;
Если угол α измеряется в радианах, то в общем случае площадь сектора круга равна R^2*α/2 (если α = 2π; то получается площадь круга π*R^2)
Поэтому Snmpc = Sdpo + Spoc - Sdpn =
= R^2*sin(π - α)/2 + R^2*α/2 - (R√2)^2*(α/2)/2 = R^2*sin(α)/2; 
Поскольку высота PH = R*sin(α) = P1O (см. условие задачи про точку P1), то всё доказано.
Sdpo = Sdp1o;
Если точка Q не совпадает с C, то это просто означает
Sdpq = Sdpo + Sdqo (или минус, в зависимости от того, где точка Q)
 

---