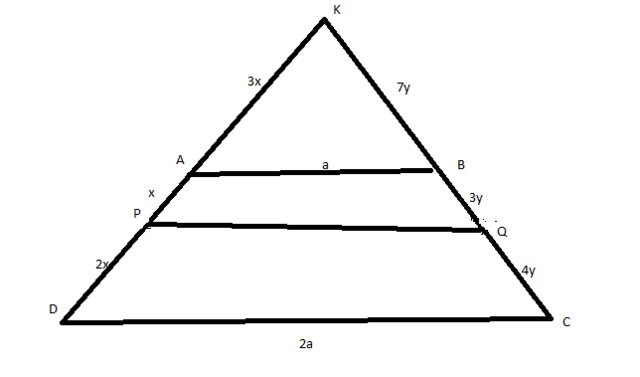
Дана трапеция АВСД : АВ || СD, CD=2AD.
DP : PA = 2, BQ : QC = 3 : 4
Найти отношение площадей четырёхугольников ABQP и CDPQ.
Решение. ( см. рисунок)
Обозначим AB=a, CD=2a. Продолжим боковые стороны трапеции до пересечения. Получим треугольник DКC.
AB- средняя линия этого треугольника, так как AB || CD и СD=2AB.
Значит DA=AК и CB=КB.
Обозначим АР=x, тогда DР=2х ( см. условие DP : PA = 2) и AD=3x=AK
ВQ=3y, тогда QC=4y и ВС=7у=КВ.
Обозначим высоту трапеции h и найдем площадь трапеции S=(a+2а)h/2=3ah/2.
Отсюда ah=2S/3
Высота треугольника DKB равна 2h, высота треугольника АКВ равна h.
(АВ- средняя линия треугольника DKB)
Площадь треугольника КАВ: ah/2=S/3.
Площадь треугольника КDC: (2a·2h)|2=2ah=4S/3
Найдем площадь треугольника КАВ по другой формуле: половина произведения сторон на синус угла между ними (АК ·КB·sinα)/2, где α- угол между АК и КВ.
Приравняем найденные площади треугольника КАВ:
S/3=(3х·7у·sinα)/2⇒ x·y·sinα=2S/63.
Найдем площадь треугольника КPQ по той же формуле: половина произведения сторон на синус угла между ними (РК·KQ·sinα)/2.
Получим (4х·10у·sinα)/2= 20х·у·sinα=( заменим х·у·sinα на 2S/63)=40S/63
Площадь четырехугольника АВQP найдем вычитая из площади треугольника PKQ площадь треугольника КАВ:
S₁=40S/63-S/3=19S/63.
Площадь четырехугольника CDPQ найдем вычитая из площади треугольника KDC площадь треугольника КQP:
S₂=4S/3-40S|63=44S|63
Находим S₁:S₂=19S/63 : 44S/63=19/44.
Ответ 19:44