Переведем данные в систему СИ
m=0.06кг
ρ воды=1000 кг/м^3
ρ дерева=750 кг/м^3
Условие требует внимания.
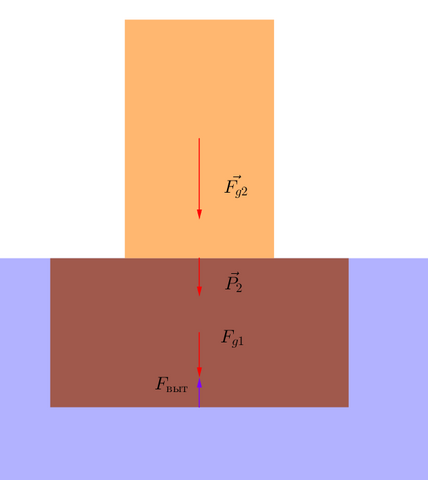
Сказано, что кубик ПЛАВАЕТ в воде, это означает что он ЦЕЛИКОМ погружен в воду, однако равнодействующая удерживает его на плаву, при этом он не тонет, не всплывает
Чтобы груз потонул необходимо чтобы вес тел превысил выталкивающую силу.
В виде уравнения это выглядит следующим образом
Fa - сила архимеда
F_a\[[1]" alt="P>F_a\[[1]" align="absmiddle" class="latex-formula">
На воду давит деревянный грузик, а на него своим весом давит другой, который мы кладем сверху,
Таким образом общий вес складывается из силы тяжести обоих грузов, теперь решим уравнение [1]
m-масса деревянного груза
M-масса груза который кладем
V-объем деревянного груза(он польностью погружен))
ρ 1 - плотность воды
ρ 2- плотность дерева
F_a\\
mg+Mg>\rho_1 gV\\
Mg>\rho_1 gV-mg\\
M>\rho_1 V-m; V=\frac{m}{\rho_2}\\
M>\frac{\rho_1 m}{\rho_2}-m\\
M>\frac{1000*0.06}{750}-0.06>0.08-0.06>0.02" alt="P>F_a\\
mg+Mg>\rho_1 gV\\
Mg>\rho_1 gV-mg\\
M>\rho_1 V-m; V=\frac{m}{\rho_2}\\
M>\frac{\rho_1 m}{\rho_2}-m\\
M>\frac{1000*0.06}{750}-0.06>0.08-0.06>0.02" align="absmiddle" class="latex-formula">
Ответ получен, масса должна быть больше 0.02 кг или 20 гр
