Отрезок ВМ медиана треугольника АВС. Докажите, что справедливо следующее неравенство:...

Question

Отрезок ВМ медиана треугольника АВС. Докажите, что справедливо следующее неравенство: ВМ<0,5(АВ+ВС)

Answer 1

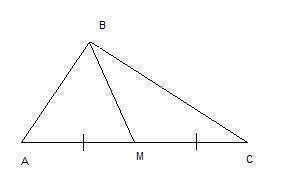
Рассмотрим треугольник АВМ. Зная, что каждая сторона треугольника меньше суммы двух других сторон, можно записать:
ВМ<АВ+АМ<br>Для треугольника ВМС можно так же записать:
ВМ<ВС+МС, но АМ=МС, т.к. ВМ - медиана, поэтому можно записать как<br>BMBM2ВМBM<<span>0,5(AB+BC)

---

Comments

ВМ<ВС+МС, но АМ=МС, т.к. ВМ - медиана, поэтому можно записать как<br>BMBM<BC

---

А откуда это? что-то не могу понять...

---

ВМ<АВ+АМ<br>ВМ<ВС+МС<br>так как АМ=МС, получается, что
BMBMэти две строки складываем и получаем
2ВМ<AB+BC

---

не понятно, как самоудаляются АМ и МС, понятно, что они равны, но разве можно их просто так взять и сократить?