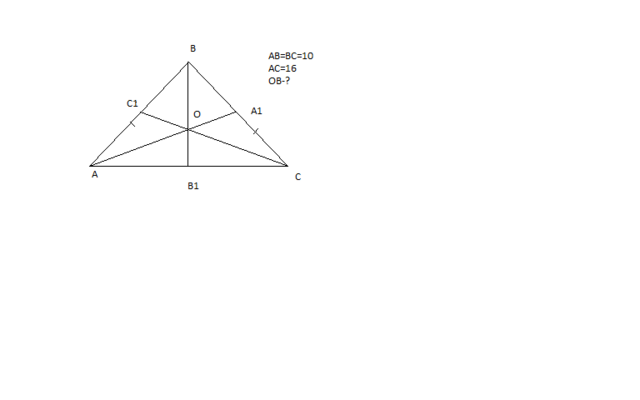
В равнобедренном треугольнике медиана, проведенная к основанию, является также и высотой. Рассмотрим получившийся прямоугольный треуг-ик АВ1В.
Здесь АВ1=СВ1=16:2=8 (т.к. ВВ1 - медиана). По теореме Пифагора в АВ1В находим неизвестный катет ВВ1:
BB1=√AB² - AB1² = √100-64=√36=6
Зная, что медианы треугольника АВС пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины, выразим ОВ.
ОВ : ОВ1 = 2 : 1 (всего частей получается 2+1=3). Если ВВ1 = 6, то каждая из трех частей равна 6:3=2. На ОВ приходится 2 части, значит, ОВ=2*2=4.