Задача не стоит своих балов, имхо).
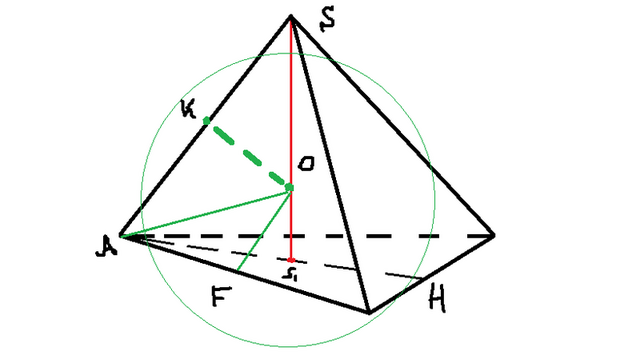
Красный - высота. K и F - точки касания. AO - расстояние по условию. OF, OK - радиусы. Для очень придирчивых - вся основа решения, т.е. после введения углов, лежит в плоскости AS1S. Из треугольника AOF: a/2=sqrt6. Тогда a=2sqrt6. Это сторона основания. Тогда AH=2sqrt6*sin60*=3sqrt2
S1F=(3sqrt2)/3=sqrt2
OS1=1
угол AOS1=k
угол AOK= l
угол KOS=b
cos(k)=OS1/AO=1/3
cos(l)=OK/AO=sqrt3/3
b=pi-arccosk-arccosl
cosb=cos(pi-arccos(k)-arccos(l))= -cos(arccos(k)+arccos(l))
Есть формула подсчета этого: arccos(k)+arccos(l)=arccos(k*l-sqrt(1-k^2)*sqrt(1-l^2)), где k+l >0
Я не буду приводить расчеты, тут все подставляется. cos(b)=(4-sqrt3)/9 = OK/OS. Отсюда находится OS. Вся высота пирамиды = OS+OS1 = (4+8sqrt3)/(4-sqrt3).
P.S. sqrt - квадратный корень из