1. Основание пирамиды - квадрат со стороной 4 дм. Две боковые грани пирамиды...

Question

68 просмотров

1. Основание пирамиды - квадрат со стороной 4 дм. Две боковые грани пирамиды перпендикулярны плоскости основания, а две другие - наклонены к ней под углом 60(градусов). Найдите объем этой пирамиды.
2. В правильной пирамиде периметр основания равен 18 см, а боковое ребро - 5 см. Найдите боковую поверхность этой пирамиды.
Буду очень благодарен.

Геометрия Foreverson_zn (114 баллов) 19 Март, 18 | 68 просмотров

Дан 1 ответ

Правильный ответ

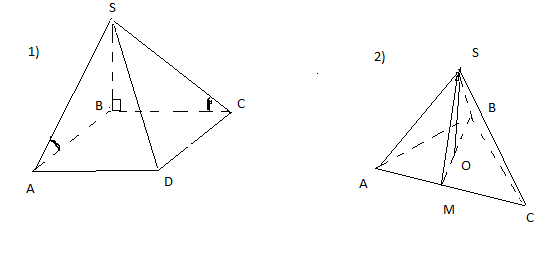
1) См. рисунок. АВСD- квадрат, $SB\perp (ABCD)$
Найдем линейный угол двугранного угла между боковой гранью SCD и плоскостью основания ABCD.
Так как ABCD- квадрат, то $CB\perp CD$
По теореме о трех перпендикулярах наклонная $SC\perp CD$
Значит, угол SCB- линейный угол двугранного угла между боковой гранью SCD и плоскостью основания. Аналогично, угол SAB- линейный угол двугранного угла между боковой гранью SAD и плоскостью основания ABCD.
$\angle SCB=\angle SAB=60 ^{o}$

Из прямоугольного треугольника SAB: SA=8 (катет АВ, лежит против угла в 30⁰ и равен половине гипотенузы), и по теореме Пифагора SB²=SA²-AB²=8²-4²=48
SB=4√3

V=AB²·SB/3=64√3/3 кв. дм.

2) Вершина правильной пирамиды S проектируется в центр описанной окружности О.
Периметр правильного треугольника равен 18, значит одна сторона равна 6=18:3 см. Треугольник ASC- равнобедренный АС=6, SA=SC=5
Высота SM этого треугольника (апофема пирамиды) равна 4 по теореме Пифагора из треугольника SAM: SM²=SA²-AM²=25-9=16, SM=4
Боковая поверхность пирамиды- сумма площадей боковых граней. Все боковые грани SAC, SAB, SBC- равные между собой треугольники.
S=3·1/2·AC·SM=3/2·6·4=36 кв.см

nafanya2014_zn (414k баллов) 19 Март, 18