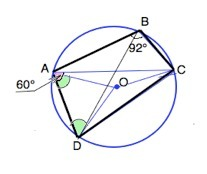
Сумма противоположных углов вписанного в окружность четырехугольника равна 180°⇒
∠ АDC=180°-92°=88°
Для решения вспомним:
Вписанный угол равен половине центрального, опирающегося на ту же дугу.
Соединим центр окружности О с А, D и C.
Центральный угол DOC опирается на ту же дугу, что ∠САD.
∠DOC=2 ∠САD=120°
∆ DOC- равнобедренный, его углы при основании CD равны (180°-120°):2=30°
∠ВDА=∠CDA-∠ODA=88°-30°=58°
В равнобедренном ∆ AOD углы при основании AD равны 58°, ⇒ ∠AOD=180°-2•58°=64°
Искомый вписанный ∠АBD равен половине центрального ∠АОD.
∠АВD=64°:2=32°