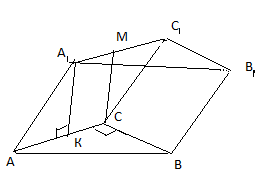
Дана наклонная призма АВСА₁В₁С₁.
Треугольник АВС - прямоугольный равнобедренный, АВ=ВС=7.
Плоскость (АСС₁А₁) перпендикулярна плоскости АВС.
Проведём А₁К перпендикулярно АС, СМ параллельно А₁К,
СМ перпендикуляр к АС и ВС перпендикуляр к АС, значит угол МСВ- линейный угол двугоранного угла между плоскостями АСС₁А и АВС.
Угол МСВ=90⁰
,
АС перпендикуляр к ВС, АК- проекция АА₁ , по теореме о трех перпендикулярах АА₁ перпендикуляр к ВС.
Значит и СС₁ перпендикуляр в ВС. Четырехугольник ВВ₁С₁С- прямоугольник. Его площадь равна 56. Катет ВС=7, значит боковые ребра призмы 8
7*8=56
Из прямоугольного треугольника АА₁К зная угол А₁АК=45⁰ ( по условию) найдем высоту А₁К=4√2
V=S·H=1/2 АС·ВС·А₁К=1/2·7·7·4√2=98√2 кв ед.