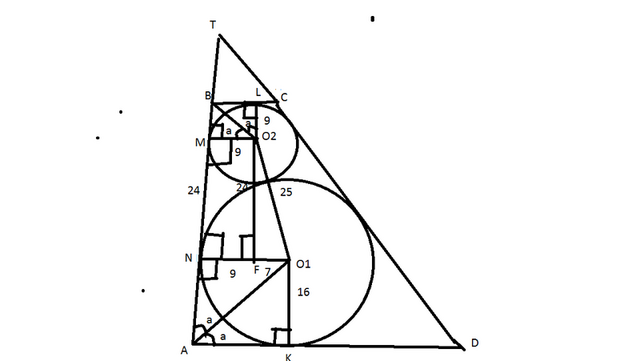
Из рассуждений представленных на рисунке и сделанных построений видно что:
NM=sqrt(25^2-7^2)=24
Продлив стороны трапеции до пересечения в точке T,то угол A=B ,как соответственные,откуда угол MBL=180-A как смежный угол.
Прямоугольные треугольники MO2B и BO2L равны по общей гипотенузе и катетам равными как радиусы окружности,по той же причине равны треугольники NAO1 и AKO1
Откуда угол NAO1=KAO1=a, угол O2BM=O2BL=(180-A)/2= (180-2a)/2=90-a
Откуда угол BO2M=NAO1=a
Для того чтобы наглядно показать ,что решение охватывает все случаи возможных трапеций,возьмем в качестве параметра угол a (что вдвое меньше угла основания)
Тогда боковая сторона будет представляться выражением:S=16/tga+9*tga+24,выделяя полный квадрат получим: S=(4/√tga -3√tga)^2+48 ,тк квадрат не отрицателен,то очевидно наименьшее значение когда: 4/√tga-3*√tga=0 ,то Smin=48
Ответ:48
Теперь я немного дополню свое решение найдя ради интереса сам угол a!!!
4/√tga-3√tga=0
заменим: √tga =t >0 tga>0 что верно тк это угол острый.
4/t-3t=0
4-3t^2=0
t^2=4/3
То есть
tga=4/3
То есть угол не так хорош как нам казалось.
Если для интереса посмотреть каков же примерно это угол,то получим:53 градуса с копейками. А сам угол основания около 106 градусов,а значит наша трапеция нестандартного вида.