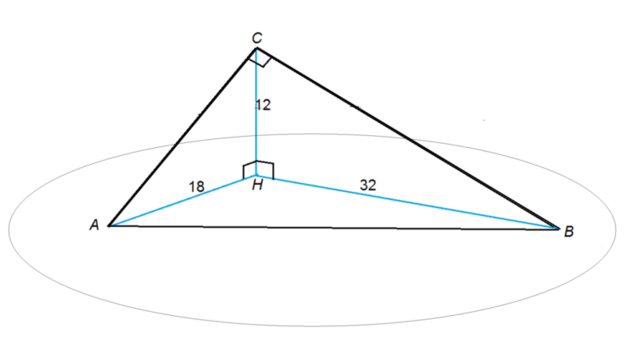
Из точки, находящейся на расстоянии 12 см от плоскости, проведены к ней две наклонные, угол между которыми 90 градусов. Проекции этих наклонных на плоскость равны 18 и 32 см. Найдите расстояние между основаниями наклонных.
Пусть данная точка будет С, основание перпендикуляра от нее к плоскости - Н. а наклонные пусть будут СА и СВ.
Так как расстояние от точки до плоскости измеряется длиной перпендикулярного к ней отрезка, треугольники АСН и ВСН - прямоугольные.
По т.Пифагора найдем АС²:
АС²=АН²+СН²= 324 + 144 = =
468
ВС²=ВН²+СН²=1024+468=
1168
Δ АСВ - прямоугольный по условию ( угол между наклонными 90°)
Его гипотенуза АВ и есть искомое расстояние.
АВ²=АС²+ВС²=468+1168=1636
АВ=√(4*409)=
2√409 см