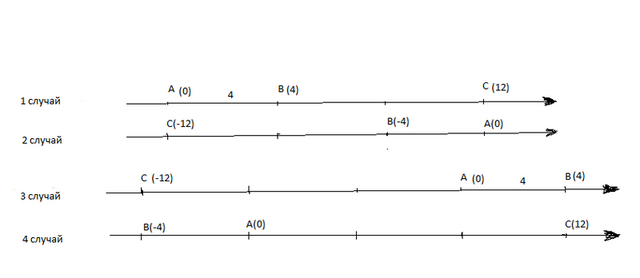
Расположим точки А, В и С на координатном луче. Точка А пусть совпадает с началом отсчета. Координата точки А (0). Точка В может быть расположена как слева так и справа от А, поэтому координаты точки В могут быть (4) или (-4).
Точка С расположена справа или слева от А - ее координаты (12) или (-12).
Всего 4 случая расположения точек А,В и С ( см. рисунок)
1) Если точка Z слева от точки А, то ZA+ZB+ZC= ZA+(ZA+AB)+(ZA+AC)=3ZA+4+12, что по условию равно 19. 3 ZA+16=19, ZA=1
Точка Z расположена слева от А на расстоянии 1, значит её кордината Z(-1)
Если точка Z расположена между А и В, то ZA+ZB+ZC таково, что ZA+ZB=AB=4, тогда 4+ZC=19, ZC=15 Невозможно, так как АС=12,
если Z расположена между В и С, тогда ZB+ZC=8
ZA+ZB+ZC=ZA+8
ZA+8=19,
ZA=11
Значит, точка Z имеет координату 11
ZA=11, ZB=7, ZC=1 в сумме 19.
Если Z расположена за точкой С, то AZ=AC+CZ, BZ=BC+CZ
AZ+BZ+CZ=AC+CZ+BC+CZ+CZ=12+8+3CZ не может равняться 19,
Итак в первом случае Z(-1) или Z(11)
2) случай аналогично, Z(1) или Z(-11)
3) случай и 4) случай.
Если точка Z расположена между точками В и С, то расстояние ZB+ZC=16
Значит ZA+ZB+ZC=19,
ZA+16=19,
ZA=3
как слева так и справа от А, поэтому Z(-3) или Z(3) как в случае 3, так и в случае 4.