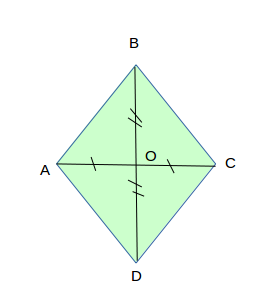
Дано: ABCD - ромб, BD = 48 см, AC = 14 см.
Найти: AB - ? r - ?.
Решение:
Диагонали пересекаются в точке О. Ромб имеет 4 равны прямоугольных треугольников.
С прямоугольного треугольника ABO (∠ AOB=90°):
OB = BD/2 = 48/2=24 см; AO = AC/2 = 14/2= 7 см
по т. Пифагора:
AB² = АО² + ВО²
АВ=√(АО²+ВО²)=√(24²+7²)=√625 =
25 см
Определим с площади S = a*h высоту, и для этого радиус вписанной окружности
S=d₁*d₂/2 = 48*14/2 = 336 см².
h=S/a = 336/25=13.44 см
Тогда радиус вписанной окружности
r = 2*h=13.44*2 =
6.72 см
Ответ: АВ = 25см; r = 6.72 см.