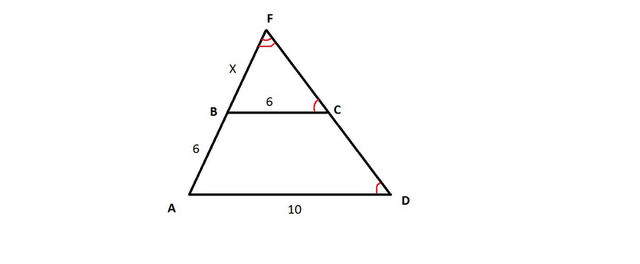
При пересечении боковых сторон трапеции ABCD, получается треугольник AFD.
рассмотрим ΔAFD и ΔBFD
Пусть BF=x, тогда AF=x+6
BC || AD -так как ABCD - трапеция, следовательно ∠FCB=∠FDA -как соответственные углы при параллельных прямых,
∠F - общий, значит ΔAFD и ΔBFD подобны по 2-м углам, следовательно можно составить пропорцию: