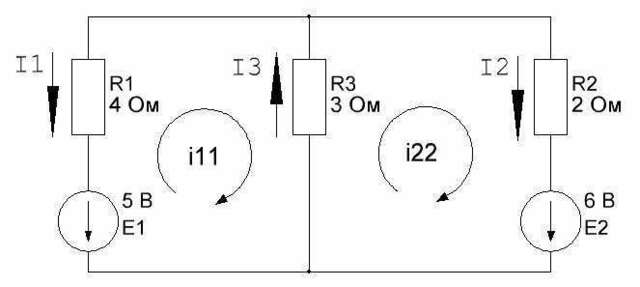
Для решения используем метод контурных токов. Перерисуем исходную схему и произвольным образом расставим на ней направления искомых токов I1, I2, I3. Если в результате решения значения каких-то токов получатся с минусом, значит на самом деле ток направлен в противоположную сторону.
Выделим на чертеже два независимых контура и в каждом из них направим контурные токи i11, i22 по часовой стрелке. Теперь для каждого контурного тока надо записать второй закон Кирхгофа: "Алгебраическая сумма ЭДС, действующая в замкнутом контуре равна алгебраической сумме падений напряжения в этом контуре". Падение напряжения на каждом элементе определяется из закона Ома для участка цепи (I=U/R ⇒ Г=I*R). Если какие-то элементы являются общими для нескольких контуров, следует учесть падения напряжения от соседних контурных токов; при этом, если в соседних контурах направление контурного тока в элементе окажется противоположным, то соответствующее падение напряжения надо взять со знаком минус.
Обходим первый контур по направлению контурного тока i11 и записываем сумму падений напряжения U11, а также сумму ЭДС E11:

Знак минус перед i22 взят потому, что ток i22 направлен встречно току i11. Знак минус перед E1 взят потому, что ЭДС E1 направлено навстречу i11.
На практике такие уравнения составлять очень просто, если придерживаться следующего метода:
Введем термин: cопротивление, общее для нескольких контуров (у нас это резистор R3), называется сопротивлением связи.
Тогда правило получения записи суммы падений напряжений в контуре можно сформулировать так: Записываем произведение контурного тока на сумму всех сопротивлений в контуре и для каждого сопротивления связи добавляем произведение этого сопротивления на величину контурного тока из соседнего контура, взятую с соответствующим знаком. Как правило, этот знак оказывается отрицательным. если все контурные токи направить по часовой (или все против часовой) стрелки.
Запишем, пользуясь предложенным правилом, уравнение для второго контура:

Осталось решить систему уравнений и определить контурные токи.

Подставим в уравнения известные значения и решим полученную систему, пользуясь правилом Крамера.


Совет: если контурные токи не выражаются целыми значениями или точно не переводятся в десятичные дроби, лучше продолжать производить вычисления в простых дробях. В противном случае проверка решения по балансу мощностей скорее всего не сойдется!
Проверка решения.
Проверку решения производим по балансу мощностей. Мощность, отдаваемая источниками ЭДС (Pe), должна равняться сумме мощностей, рассеиваемых на сопротивлениях цепи (Pr).