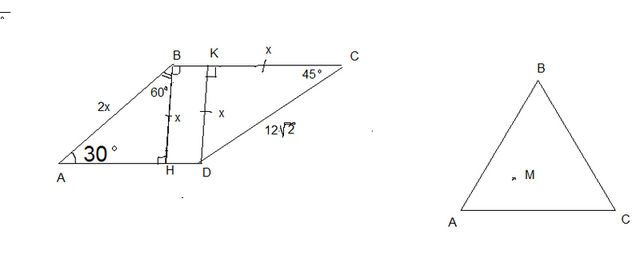
1) Проведем высоту АН и DK. Получим два прямоугольных треугольника.
Угол АВС равен 150⁰, угол НВС=90⁰, значит угол АВН=60⁰, а уго ВАН=30⁰.
В прямоугольном треугольнике против угла в 30⁰ лежит катет, равный половине гипотенузы. Высота ВН в два раза меньше стороны АВ.
Обозначим сторону АВ=2х, тогда высота ВН=х, высота DK=x.
Треугольник DKC - прямоугольный, равнобедренный. Угол DCK 45°, значит и второй острый угол треугольника 45°.
Поэтому катеты КС=KD=x,гипотенуза CD=12√2
По теореме Пифагора х²+х²=(12√2)², 2х²=288,х²=144, х=12, значит АВ=2х=24 см
Ответ. АВ=24 см.
2) Точка М на плоскости? внутри треугольника? или в произвольном месте?