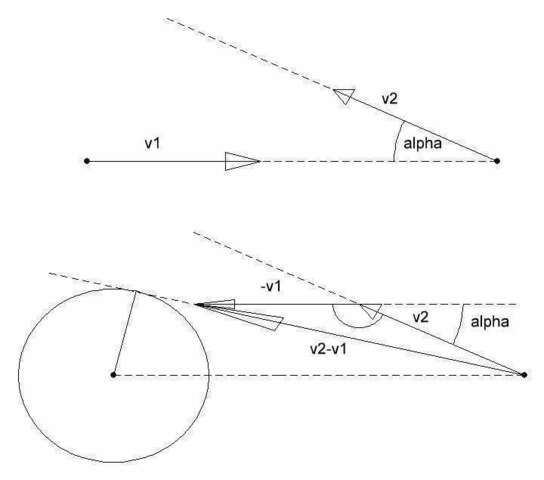
В системе отсчета, связанной с телом М1, тело М2 движется со скоростью v2 (вектор) - v1 (вектор)
величина относительной скорости вычисляется по теореме косинусов
v=корень(v1^2+v2^2-2*v1*v2*cos(pi-alpha)) = =корень(v1^2+v2^2+2*v1*v2*cos(alpha))
минимальное расстояние вычисляется из подобия треугольников по формуле
Xmin = АВ*v2*sin(alpha) / v =
=АВ*v2*sin(alpha) / корень(v1^2+v2^2+2*v1*v2*cos(alpha)) =
=L*sin(alpha) / корень((v1/v2)^2+1+2*(v1/v2)*cos(alpha))
построением найти это расстояние можно, опустив перпендикуляр из точки М1 на прямую, проходящую через М2 и параллельную v2 (вектор) - v1 (вектор)
искомая длина = длина перпендикуляра
рисунок прилагается