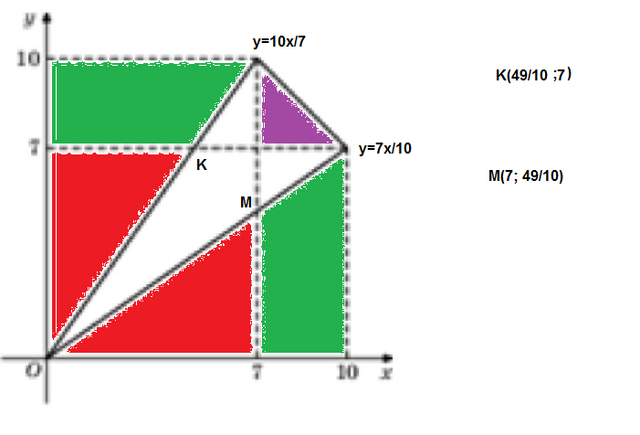
Можно составить уравнения прямых, ограничивающих равные стороны треугольника
Обе прямые проходят через начало координат.
Общий вид такой прямой у-kx.
Подставим координаты точки (10; 7)
получим 7=10k, k=7/10
у=7x/10
Аналогично вторая прямая имеет уравнение у=10x/7
Находим координаты точек К и М:
при х=7 у=7·7/10=49/10 K(7; 49/10)
Аналогично при у=7 находим координаты точки М: М(49/10; 7)
Площадь треугольника равна
сумме следующих площадей.
1) из площади квадрата со стороной 7 вычитаем две площади (красные) треугольника со сторонами 7 и 49/10
2) Из площадей прямоугольников со сторонами 3 и 7 вычитаем площадь трапеции с основаниями 49/10 и 7 и высотой 3
3) площадь прямоугольного треугольника с катетами 3
S= 49- 7·49/10 + 2· 3·7- (49/10+7)·3 + 3·3/2=255/10=25,5