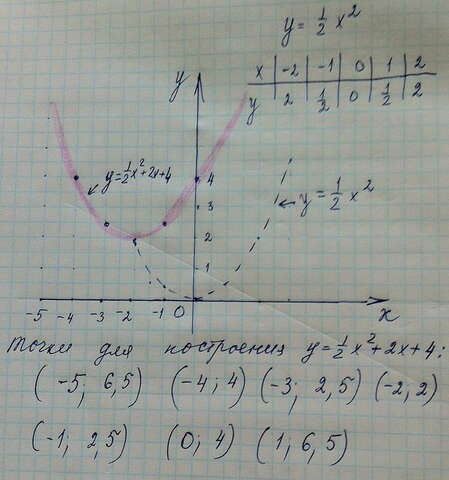Выделим полный квадрат в квадратном трехчлене. Вынесем 1/2 за скобки:
1/2(х²+4х+8)=1/2(х²+4х+4+4)=1/2(х²+4х+4) + 1/2·4=1/2(х+2)²+2
Графиком функции у=1/2 (х²+2)+2 является парабола ветви которой направлены вверх, вершина имеет координаты (-2;2)
Парабола не пересекает ось Ох, так как дискриминант квадратного трехчлена 1/2х²+2х+4 отрицательный. D=2²-4·(1/2)·4<0<br>Парабола у=1/2 (х²+2)+2 принимает наименьшее значение в вершине, т.е при х=-2 у=2
См график на рисунке.