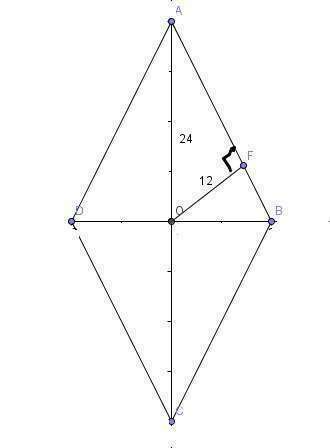
1. Расстояние между точкой и прямой есть перпендикуляр, таким образом угол ОFА=90 градусов.
2. Диагонали ромба точкой пересечения делятся пополам и являются биссектрисами его углов. То есть: АО=AС/2=24
3. Если в прямоугольном треугольнике катет равен половине гипотенузы, то угол который лежит против этого катета равен 30 градусов.
4. Противоположные углы ромба равны и сумма двух не равных равна 180 градусов.
Итак, рассмотрим прямоугольный треугольник АОF, катет ОF равен половине гипотенузы АО, следовательно угол ОАF=30 градусов. Значит угол А ромба равен 2*30=60 градусов, а угол В=180-60=120 градусов.