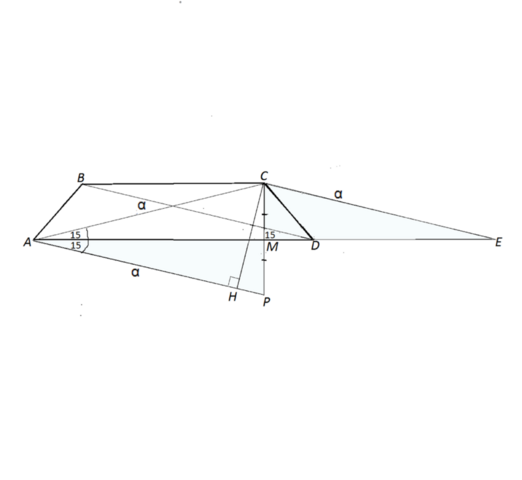
.Диагональ равнобокой трапеции равна α (альфа) и составляет угол 15° с основанием. Найти площадь трапеции.
Для решения данной задачи нужны в основнои рассуждения.
В равнобокой трапеции диагонали равны и каждая составляет с основанием одинаковый угол.
Из вершины С проведем параллельно диагонали BD прямую до пересечения с продолжением АD.
Обозначим точку пересечения Е.
Четырехугольник ВСЕD - параллелограмм, т.к. противоположные стороны параллельны, и СЕ равно BD .
Следовательно, DE=ВС, и
АЕ - равна сумме оснований.
Площадь трапеции АВСD равна половине произведения ее высоты СМ на АЕ - сумму оснований.
Площадь равнобедренного треугольника АСЕ равна половине произведения его высоты на АЕ.
Высота трапеции и треугольника общая.
Площади данной трапеции и площадь получившегося треугольника равны. Опустим из С высоту СМ и отложим на её продолжении отрезок МР, равный СМ.
Соединив А и Р, получим равнобедренный треугольник АСР , т.к. треугольники АСМ и АМР равны по двум сторонам и прямому углу при М между ними.
В треугольнике АСР угол при вершине А равен 30 градусам ( 15+15).
Из С опустим на сторону АР высоту СН.
Её длина, как длина катета, противолежащего углу 30 градусов, равна половине АС и равна α/2
S Δ АСР равна АР*СН:2=α·α/4=α²/4
Треугольник АСР равен треугольника СМЕ, и площадь треугольника АСР равна площади треугольнка АСЕ, т.е. равна площади трапеции.
Ответ: Площадь трапеции равна α²/4