В равнобедренном треугольнике АВС (АВ = ВС) угол при вершине В равен 20 градусов. **...

Question

В равнобедренном треугольнике АВС (АВ = ВС) угол при вершине В равен 20 градусов. На сторонах АВ и ВС выбрали соответственно точки Е и F, и угол АСЕ = 60 градусов, угол САF = 50 градусов. Определить вечилину угла CEF

Answer 1

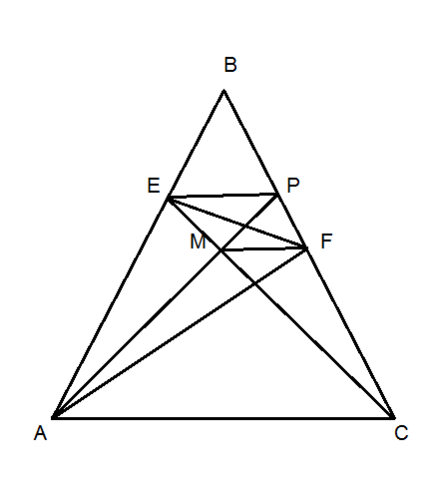
Проведем отрезок EP || AC.

Пусть М - точка пересечения отрезков АР и СЕ. Тогда треугольники ЕРМ и АМС является равносторонними. Итак, ЕР = ЕМ, и МС = АС. Но угол CAF = 50°, угол ACF = 80°, поэтому угол AFC = 50°. Следовательно, FC = AC = MC.

Поскольку  угол MCF = 20°, то угол CFM = углу CMF = 80°. А значит, 
угол PFM = (180°-80°)=100°. Но угол РАС = 60°, угол PCA=80°, итак угол MPF = 40°. Поэтому угол PMF = 40°. 
Отсюда следует что PF = MF. Треугольник EPF = треугольнику EMF на основе равенства трех соответствующих сторон. Следовательно, Угол MEF = углу PEF = 1/2 * угол MEP = 1/2 * 60° = 30°

Ответ: 30°.

---

Comments

Вы второе решение посмотрите, пока его не удалили( :)), там человек явно не разобрался в решении, ну и написал вначале, что эти отрезки параллельны. Это - как пояснение, почему я на это обращаю внимание.

---

Я дам всем, кто интересуется, ссылку на эту задачу в задачнике Прасолова, номер 12.60. Там решение совершенно другое, и основано на свойствах правильного 18-угольника. Для того, чтобы разобраться в решении у Прасолова, надо знать теорему Чевы в тригонометрической форме. Или можно доказать самостоятельно, что у правильного 18-угольника диагонали A18A6; A17A4; и большая диагональ A1A10 пересекаются в одной точке. Задачка эта очень полезная, и если её решить, эта задача решается в одно действие.