Поскольку AN - биссектриса угла В, то ∠BAK=∠ KAN.
∠BNK=∠KAN как накрест лежащие ⇒ ∠BAK=∠BNK.
А значит мы получим, что треугольник ABN равнобедренный.
А значит AB=BN.
Треугольник ΔABK=ΔBKN (по двум углам и стороне между ними: BN=AB, ∠BNK=∠BNK, ∠ABK=∠NBK поскольку BK биссектриса).
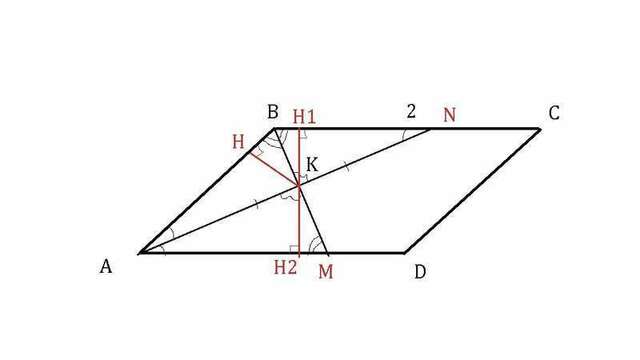
Проведем высоту в треугольнике KBN из К на сторону BN.
Поскольку ΔABK=ΔBKN, то и высоты равны KH=KH₁=1.
Если опустить высоту из точки К до стороны AD, то получим высоту KH₂.
ΔKBN=ΔAKM (по стороне и двум прилежащим к ним углам: AK=KN, ∠KAM=∠BNK, ∠AKM=∠BKN - вертикальные).
Значит KH₁=KH₂=1 ⇒ H₁H₂=1*2=2
Sabcd=BC*H₁H₂=2*2=4