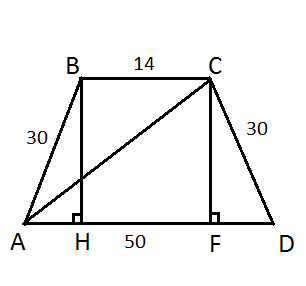
Смотри рисунок :)
Проведем две высоты трапеции - BH и CF
BC=HF=14см
AH=FD, т.к. трапеция равнобедренная, значит на каждое приходится по 18см (50-14=36 ; 36/2=18)
Рассмотрим треугольник DCF
Он прямоугольный
Мы знаем CD и FD, следовательно можем смело искать CF по теореме Пифагора:
30^2 = 18^2 + CF^2
900=324 + CF^2
CF^2 = 576
CF = 24
Теперь рассмотрим треугольник FAC
Он тоже прямоугольный
Мы знаем AF (18+14=32) и выяснили, что CF=24
Значит можем искать саму диагональ AC тоже по теореме Пифагора:
AC^2=1024+576=1600
AC=40