В1. 90°, так как вписанный угол, опирающийся на полуокружность, прямой.
В2. ∠АВС вписанный, поэтому большая дуга АС равна 240°, тогда ∪АВС = 360° - 240° = 120°,
∠АОС - центральный, опирается на дугу АВС, значит ∠АОС = 120°
В3. NM = KM - так как отрезки касательных, проведенных из одной точки, равны.
В5. Пусть вписанный угол равен х градусов, тогда центральный - 2х.
2x - x = 40°
x = 40°
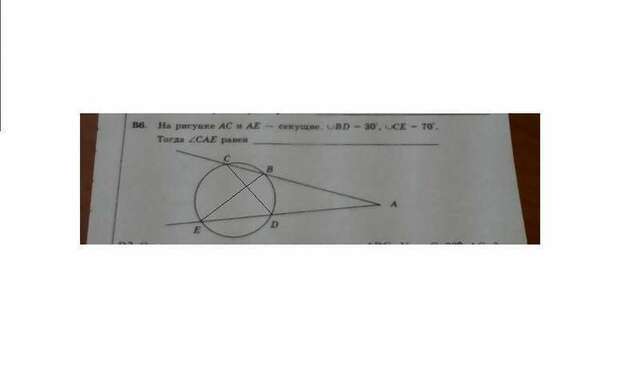
В6. ∠BED = 1/2∪BD = 15°
∠CBE = 1/2∪CE = 35° - внешний угол ΔBED, равен сумме двух внутренних углов, не смежных с ним.
∠СВЕ = ∠BED + ∠BAE
∠BAE = 35° - 15° = 20°
В7. ΔАВС прямоугольный, найдем второй катет по теореме Пифагора:
ВС = √(АВ² - АС²) = √(25 - 9) = √16 = 4 см
Рabc = 3 + 4 + 5 = 12 см
Sabc = АС·ВС / 2 = 3 · 4 / 2 = 6 см²
В8. 2. Сначала найдем градусную меру всех дуг:
∪МК = 180°, так как МК - диаметр,
∪РК = 100°,
∪NP = ∪NK - ∪PK = 140° - 100° = 40°
∪MN = 180° - 100° - 40° = 40°
Вписанный угол равен половине дуги, на которую опирается:
∠NMK = (100° + 40°)/2 = 70°
∠MKP = (40° + 40°)/2 = 40°
∠KPN = (180° + 40°)/2 = 110°
∠PNM = (100° + 180°)/2 = 140°