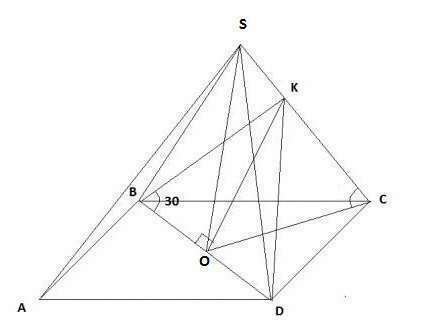
Пусть пирамида ABCDS в которой высота SO падает в точку пересечения диагоналей основания.
Проведем на ребро SC перпендикуляры BK и DK, тогда угол BKD равен 120 градусов.
BО=√6·√(2)/2=√3
Проведем биссектрису KО, она же является перпендикуляром к стороне BD. Тогда из прямоугольного треугольника ОBK, КО=1 (угол ОBK 30 градусов)
Из прямоугольного треугольника КОС найдем синус угла КСО
sinКСО=KО/CО=√3/3
cosα=√[1-(3/9)]=√6/3
tgα=√2/2
Из прямоугольного треугольника SOC
SO=√6/2
Тогда высота боковой грани по теореме Пифагора =√3
Sбок=4·√6·√3/2=6√2
Успехов в учебе!
Математика- самая красивая, гармоничная, правильная и справедливая модель нашего мира и нас в нем.©