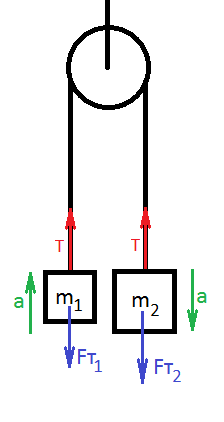
Очевидно, более тяжелый груз поедет вниз, а более лёгкий - наверх. Так как нить нерастяжимая, ускорения обоих грузов равны по модулю. На каждый из грузов действует сила натяжения нити T (силы, действующие на грузы, равны по третьему закону Ньютона) и сила тяжести Fт = mg.
Запишем выражения по второму закону Ньютона:
m1 a = T - m1 g; T = m1 a + m1 g
m2 a = m2 g - T; T = m2 g - m2 a
Приравнивая значения T, получаем
m1 a + m1 g = m2 g - m2 a
(m1 + m2) a = (m2 - m1) g
a = g * (m2 - m1)/(m1 + m2)
T = m1 a + m1 g = (m1 m2 - m1^2 + m1 m2 + m1^2)/(m1 + m2) g = 2m1 m2 / (m1 + m2) g
Осталось определить силу давления на ось T'. По третьему закону Ньютона она должна уравновешиваться силой натяжения нити, на которой висит блок. Блок тянут вниз две силы T, тогда сила натяжения нити, на которой висит блок, равна 2T, что по модулю равно силе давления T'.
Ответ. a = g * (m2 - m1)/(m1 + m2) = g/5 = 1.96 м/с2, T = 2m1 m2 / (m1 + m2) g = 0.24 кг * g = 2.35 Н, T' = 2T = 4.70 Н